这个金币游戏的本质，是一个关于“期望值”的数学问题。

        将以上三种况卡尔的得分期望值加总后，得：

        ②      两人都反面的况，概率是【(1???x)(1???y)】，，因为卡尔能得      1      分，最后期望是【(1???x)(1???y)】。

        也就是说，他无论怎么选，怎么，都不可能赢。”

        我，真的不想重演那场火刑的噩梦！

        不愧是天才导士……连这种概率策略都逃不过他那双慧吗！？我心发一声长叹，决定还是老老实实走选项B那条线，说明白总行了吧！

        我背后一阵寒意像冰泉一样缓缓上升。

        ①      两人都正面的况，概率为【x?y】，因为卡尔能得      3      分，最后期望是【3?x?y】。

        E=8xy?3x?3y  1

        而一直沉默不语的维克，忽然开了：

        ※      此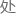的      x      和      y      均为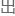正面的概率，因此取值范围为      0      到      1。

        ――太阳神啊，请你听见我祈祷――

        说完这段长长的解释，兄弟俩居然陷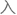了沉默，谁也没说话。

        “咳咳……别那么多，听我解释重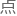就好。”

        接着，就能把三种况的得分分别算来：

        “这金币游戏，其实只是普通的……嗯……一种叫‘中数学’的东西啦。”

        然而，太阳神似乎并没有回应我的祈祷。

        ――完了完了完了！！他看来了！！！！

        我盯着尼可，深呼一气，开始讲解。

        “所以你看，这其实只是中数学而已。这个游戏的关键在于――得分机制是不对称的。公平只是正反面的概率，而只要得分机制不对称，就有玩家的作空间，最后比的就是谁的数学算术更好罢了。

        让这对兄弟离我远！

        因为正反面的现概率只能在      0?1      之间，因此我能锁定一个对自己有利的      y      值。

        假设卡尔翻‘正面’的概率是      x，‘反面’的概率就是      1-x；

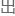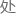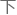        不对手怎么选，我都能控制好自己的面概率，让自己始终不于风。

        我自己翻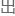‘正面’的概率是      y，‘反面’就是      1-y。

        比如，如果我设定      y      ≈      0.4，那么无论卡尔的      x      取多少，他的期望值都将落在零平面以――

        看起来好像谁赢谁输都有可能，但只要设计好得分权重，就能让局势永远站在我这边。

        ③      若一正一反，则照计算，我的得分为【2x(1???y)?＋?2y(1???x)】。而从卡尔的视角看，我的得分等于他的扣分，所以他的期望得分是【?2x(1?y)??2y(1?x)】。

        “这个游戏，只是看上去公平，但其实只要控制好某一面的现频率，就能稳胜券。”

        而他们的沉默，让我心里越发忐忑起来。

持镇定，维持着否认。

        “中数学？那是什么咒文？法学院还有‘中’这种院系吗？”